1　概述

　　机械加工的目标是追求加工精度、成本和效率的最佳组合，为了实现该目标，急需研究开发的关键技术之一就是加工精度在线测量技术，特别是在多品种小批量生产条件下，研究先进的在线测量技术意义尤其重大，因为在线测量是加工测量一体化技术的重要组成部分，是保证零件质量和提高生产率的重要手段。国外很早就已经认识到在线测量技术的重要性而进行了大量的研究，并且在生产实际中得到了大量的应用。
　　零件加工精度的在线测量分为两种情况，一是在加工过程中直接测量工件加工表面，加工过程一结束，就能得到所需要的精度指标[1],这是在线测量最理想的情况；二是加工过程结束后，工件仍然安装在机床上，用合理的测量仪器对工件进行测量[2]。在超精密加工中，热变形对加工精度的影响是不可忽视的，因此在加工过程中恒温油淋浇或切削液冷却是必须的，在有冷却液和工件转速高的情况下，测量精度达到0.01μm的传感器目前还没有，因此在超精密加工中，零件加工精度的检测主要是采用传统的离线测量方法，而离线测量的费用在很多情况下等于甚至超过零件的加工费用。
　　基于上述原因，本文对第二种情况进行研究，以实现零件的在线测量，其实质是把车床作为坐标测量机使用。由于研制的亚微米超精密车床运动部件的运动精度是很高的，甚至比很多测量仪器和测量机的运动精度还高，如果把机床和合适的测量仪器有机地接合起来，即可实现零件加工精度的在线测量，这样机床即可作加工用，又可作测量用，扩大了机床的应用范围，又解决了零件的测量问题[3]。现在机械加工质量保证的发展趋势是：通过用在线测量全部代替离线测量和统计质量控制使质量保证更靠近加工过程，保证零件从加工设备卸下就是合格品，当然这需要一个前提即在线测量的效率和精度必须得到保证，这样综合决策和必要的补偿就能在最小的时间延迟内得以实现。因此研究零件加工精度的在线测量技术具有重要的现实意义。

2　影响在线测量精度的误差源分析

　　在线测量的目的是检查加工零件的精度指标是否符合要求，如果符合要求，则卸下工件，否则进行必要的补偿加工，直到工件加工精度合格，我们知道要准确测量零件的加工精度，测量设备的精度必须比被测量零件的精度高一个量级即10倍原则，在超精密加工中，加工环境和在线测量环境相差不大，要想保证在线测量的精度，只能通过误差补偿来实现，也就是说通过误差补偿来在线测量不补偿加工的零件是能保证测量精度的（误差补偿能使零件的加工精度提高一个量级），通过误差补偿来测量补偿加工的零件则不能满足10倍原则，但是应用误差补偿后车床在线测量的精度已足够高，还是有意义的。
　　当然，车床作为坐标测量机使用，在线测量精度也受到测量传感器的精度及测量策略和数据处理策略的影响。在该车床（采用T型布局）设计制造过程中采用了许多先进技术以减少或消除热变形误差对车床运动精度的影响，如该车床采用空气静压主轴且选用白色密玉作为主轴和轴承的材料；车床溜板采用空气静压导轨；车床主轴箱、溜板、床身和导轨均选用花岗岩材料；加工的间温度控制在20±0.1℃等，因此影响测量精度的误差源主要是机床的几何误差，共有21项即每个运动部件的6个误差和3轴之间的三个相互位置误差。21项误差如下表所示。准确迅速地对误差源进行辨识是实现高精度在线测量的基础，考虑到测量过程和加工过程的运动方式很相似（刀具由传感器或测量探针代替，当然二者的误差补偿模型也是相似的），非误差敏感方向上的误差源对测量精度的影响可以忽略，即不单独考虑δ(x)、γ(x)、δY(z)、γ(z)、δY(Ф)和α(Ф)对测量精度的影响，再加上βXZ不影响测量精度（被αZФ和βXФ包含），在机床鉴定过程中，对主轴回转精度进行了测量，实测结果为主轴的径向跳动误差δX(Ф)和轴向窜动误差δZ(Ф)均<0.05μm,与溜板直线度误差（δZ(x)≤0.18μm/100mm,δX(z)≤0.20μm/100mm)相比较小，主轴偏摆误差β(Ф)也很小，因此在线测量零件加工精度时，不单独考虑主轴回转误差对测量精度的影响。当然要想高精度在线测量大尺寸零件（大尺寸平面镜），则主轴的回转误差（如β(Ф)）必须考虑。

车床21项误差源列表

序号	符号	几何意义	序号	符号	几何意义
1	δx(x)	X轴定位误差	12	γ(z)	Z轴俯仰误差
2	δy(x)	X轴Y向直线度误差	13	δx(Ф)	主轴X向跳动
3	δz(x)	X轴Z向直线度误差	14	δy(Ф)	主轴Y向跳动
4	α(x)	X轴翻滚误差	15	δz(Ф)	主轴Z向窜动
5	β(x)	X轴偏摆误差	16	α(Ф)	主轴绕X转角误差
6	(x)	X轴俯仰误差	17	β(Ф)	主轴绕Y转角误差
7	δz(z)	Z轴定位误差	18	γ(Ф)	主轴绕Z转角误差
8	δx(z)	Z轴X向直线度误差	19	αzФ	主轴和Z轴平行度误差
9	δy(z)	Z轴Y向直线度误差	20	βxФ	主轴和X轴垂直度误差
10	α(z)	Z轴翻滚误差	21	βxz	X轴和Z轴垂直度误差
11	β(z)	Z轴偏摆误差

3　误差源辨识及建模

　　该车床主要加工圆柱面、端面、锥面和球面等零件，在不考虑主轴回转误差的情况下，在线测量圆柱面母线的形状或圆柱度误差时只需要X向误差补偿；在线测量端面时需要Z向误差补偿；在线测量锥面和球面等曲面时需要同时进行Z向和X向误差补偿，这时误差补偿模型必须是二维的。当然用3个电容传感器也可以补偿主轴回转误差对测量精度的影响，误差补偿量的辨识通常有两种方法，一是首先离线辨识各项误差源，通过一定的合成法则（如齐次坐标变换）得到机床加工空间各点的误差补偿量；二是通过测量零件已加工表面得到误差补偿量，第一种方法费时且建模过程中的假设影响建模精度，第二种方法只能补偿测量具体零件，不能把补偿区域扩大到整个加工区，本文把两种情况结合起来辨识误差补偿量，既保证精度又节省时间。

3.1　误差源辨识
　　①　X向误差补偿量的辨识：
　　影响X向测量精度的误差源有6项即：δX(z)、αZФ、β(z)、α(z)、δX(x)和β(x),X向误差补偿量表示为：

δX=δX(x)+δX(z)+αZФ.z+β(z).WZ+α(z).Wh+β(x).TZ      (1)

式中　z——Z溜板离开原点的距离；
　　　WZ——测量点在Z向离开吸盘的距离；
　　　TZ——Z向上传感器离开X溜板运动部件重心的距离；
　　　Wh——工件上测量点在竖直方向距离Z溜板（主轴箱安装在Z溜板上两者成为一体）重心的距离；
　　为了辨识误差源，在Z向100mm加工范围内车削圆柱面（X溜板静止），用传感器在刀具相对的方向测量工件母线的误差，即可得到测量圆柱面时在X向的误差补偿量δ柱X,如图1所示，影响工件母线精度的误差源有4项即：δX(z)、αZФ、β(z)和α(z),误差补偿量表示为：

δ柱X=δX(z)+αZФ淘宝特卖频道毛孔厂房网眼影瘦身霜排行榜最好什么牌子的滋润好非常好最好的遮瑕是哪个.z+β(z).WZ+α(z).Wh      (2)

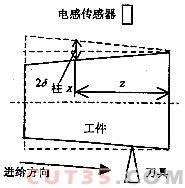
图1　圆柱母线误差测量示意图

　　这样一次就能辨识到4个误差源,由式(1)和(2)知道δX中还有δx(x)和β(x)需要辨识，β(x)需要用激光测量设备离线辨识，δx(x)则由车床全闭环系统保证。这样在测量时X向误差补偿量即能得到，即：

δx=f(x,z)=δ柱X+β(x).TZ      (3)

　　②　Z向误差补偿量的辨识：
　　影响Z向测量精度的误差分量有6项即δz(x)、β(z)、βxФ、α(x)、β(x)和δz(z),误差补偿量表示为：

δz=δz(x)+βxФ.x+α(x).Th+β(x).TX+β(z).WX+δz(z)      (4)

式中　　x——在X向离开原点的距离（端面中心）；
　　　　WX——工件上测量点在X向离开吸盘中心的距离；
　　　　Th——传感器在竖直离开X溜板运动部件重心的距离；
　　　　TX——X向上传感器离开X溜板运动部件重心的距离；

　　在测量零件端面时（Z溜板静止），影响端面测量精度的误差源有4项即βxФ、δz(x)、α(x)和β(x),用公式表示为：

δ面X=δ(x)+βxФ.x+α(x).Th+β(x).Tx      (5)

　　为了辨识这4个误差源，先车削一个直径为200mm(可适当增大直径)的端面，假设端面沿径向是对称的[3],把棱镜安装在刀架背后和刀具等高并保持和刀具沿Z向共线[4],同时把刀具换成电感传感器，首先用激光器测量几次X溜板直线度，用最小二乘法拟合出激光与X溜板运动方向的夹角，以工件中心为（以该点为基准）起点沿进给方向测量：

δ=δ传-δ直

　　式中　δ传——传感器读数；
　　　　　δ直——X溜板直线运动误差。
　　对δ序列拟合直线可得到2βxФ,同时得到端面径向母线的形状误差δ行(x)，这样就得到从工件中心到外测量端面的误差补偿量δ面Z=δ行(x)+x.βxФ,为了克服随机误差的影响，需要多次车削多次测量，由式(4)和(5)知道：Z向误差源中还有β(z)和δz(z)没有辨识，β(z)用激光测量设备离线测量辨识，δz(z)由车床全闭环系统保证，测量端面时Z向误差补偿量为：

δz=f(x,z)=δ面Z+β(z).TX      (6)

3.2　误差源建模
　　考虑到只要BP神经网络隐层节点数足够多就能以任何精度拟合任意非线性函数，并且内插精度很高，本文采用神经网络建立误差补偿模型。John C.Ziegert首先应用了这种方法，但没能解决训练样本问题[5],本文利用MATLAB5.1神经网络工具箱建立在线测量误差补偿模型，非常方便。全部网络拓补结构均采用基于Levenberg-Marquardt优化算法的BP网络，隐层用“tansig”函数，输出层用“purelin”函数。
　　①　X向误差补偿量建模：
　　以Z溜板的位置z作为网络的输入，以δ柱X作为输出，用神经网络A(结构如图2所示)拟合函数δ1X=δ柱X=f(z);以X溜板的位置x作为网络的输入，以β(z).TZ作为输出，用神经网络B拟合函数δ2X=β(z).TZ=f(x),其中δ1X=δ柱X=f(z)是测量零件圆柱度和母线直线度时的误差补偿模型；

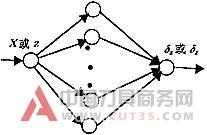
图2　单入单出神经网络拓补图

　　②　Z向误差补偿量建模：
　　以X溜板的位置x作为网络输入，以δ面Z作为输出，直接用神经网络C拟合函数δ1Z=δ面Z=f(x);以Z溜板的位置z作为网络的输入，以β(z).TX作为输出，用神经网络D拟合函数δ2Z=β(z).TX=f(z),δ1Z=δ面Z=f(x)是在线测量端面平面度时的误差补偿模型。
　　在实际加工中，经常用的区域是100mmmm×100mm,由于驱动丝杠的螺距是5mm,而直线度误差中很明显有以螺距为周期的成份，为了能准确建模，把加工区间均分为51×51个点（保证采样点有足够密度），即需要2601个训练样本，训练样本计算方法如下。
　　X向误差补偿量训练样本的计算：
　　在测量δ柱X时，得到采样点（δ柱X(zj),zj）zj=0,2,4,…,100(mm);j=0,1,…,50即在0～100mm内共采样51个点；在测量β(x).Tz时，得到采样点（δ2X(xi),xi）xi=0,2,4,…,100(mm);i=0,1,…，50即在0～100mm内采样51个点，即X向误差补偿量的训练样本为：

δ(xi,zj)=δ2X(xi)+δ1X(zj)xi、zj=0,2,4,…,100(mm)
i,j=0,1,2,…,50;                                              (7)

同样得到Z向误差补偿量的训练样本为：

δZ(xi,zj)=δ1Z(xi)+δ1Z(zj)xi、zj=0,2,4,…,100(mm)
i,j=0,1,2,…,50;                                              (8)

　　由式(7)和(8)得到车床加工空间内的神经网络训练样本为[(δX(xi,zj),δZ(xi,zj)),(xi,zj)]xi、zj=0,2,4,…,100(mm)i,j=0,1,2,…,50;
　　这样以(xi,zj)为网络输入，以（δX(xi,zj),δZ(xi,zj)）为输出用一个双输入双输出神经网络就可以拟合车床加工空间内在线测量误差补偿量模型（不包括δX(x)、δZ(z)的影响），其拓补结构如图3所示。由上面的建模过程知道：在测量球面等曲面时，X、Z方向在(xi,zj)点的误差补偿量为：

δX=δX(xi,zj)-δX(xi-1,zj-1)      (9)

δZ=δZ(xi,zj)-δZ(xi-1,zj-1)      (10)

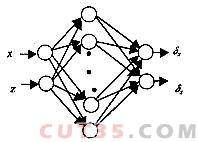
图3　双入双出神经网络拓补图

4　在线测量实验及结果分析

　　为了证明所建模型的正确性，误差补偿模型建立后，用测量精度为0.01μm电感传感器代替刀具对两种加工零件进行了在线测量：
　　①　车削一个圆柱面(母线为100mm)，在线测量工件的母线直线度，母线直线度误差为0.26μm(补偿加工后直线度为0.10μm);在主轴安装码盘的条件下，在线测量工件圆柱度误差为0.38μm(补偿加工后为0.21μm),在TAYLOR圆柱度仪上测量结果为0.40μm;
　　②　车削一个端面(直径为100mm)，在线测量工件端面的平面度误差，测量结果为非补偿零件平面度误差为0.80μm,离线测量结果为0.78μm,补偿零件的平面度误差为0.12μm。端面平面度测量原理为：数控车床的主轴转速范围为48～3000r/min无级调速，把主轴转速降至60r/min;把刀具换成电容传感器，其电压输出通过MC-1249光隔离模入接口板由计算机采样，从工件中心向外测量，在把传感器对准中心后，把传感器的值作为零点。传感器相对工件的运动轨迹为阿基米德螺线，其极坐标方程为：

ρ=-(θ+π)/2π　　　-π≤θ≤-97π

　　为了计算平面度方便，把极坐标方程化为直角坐标参数方程即：

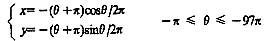
　　其中　θ=2πt　　0≤t≤48s
　　由上面方程可以看出：主轴转一圈，传感器沿与加工相反的方向径向移动1mm(X溜板移动速度范围0～200mm/min),工件半径为50mm,考虑到测头直径，采样工件48圈，采样间隔为0.1s,即每圈采10个点，采到481点时停止采样，误差补偿后得到每点的偏差分布即zi=f(xi,yi),用最小二乘法即可求得平面度误差，在工件外围区域采样间隔可以大一些。当然根据实际需要可以调整主轴转速和溜板的运动速度以得到合理的采样点分布。
　　由上面的测量结果知道，通过误差补偿后，在线测量精度是令人满意的，如果同时补偿主轴的回转误差，在线测量精度会更高。由于没有高精度测量探针，因此不能在线测量球面等曲面，如果有高精度测量探针及相应的数据处理软件，则车床完全可以作为高精度坐标测量机使用。

5　结论

　　测量结果表明：本文提出的基于神经网络的误差补偿模型能提高在线测量精度，建模简单精度高，在实际中便于使用，良好的训练样本能覆盖机床整个加工空间，为了实现在线测量的自动化，可以把测量传感器或探针储存在刀架上，如在车床上用一个转动刀架，加工时刀具靠近工件，测量时传感器靠近工件，这个转换过程可以自动进行。完全由机床本身即加工测量一体化技术自动保证零件的加工精度是制造技术发展的目标，无须质疑，在线测量技术是零件质量保证和提高生产率的重要手段，在机械加工中扮演着十分重要的角色，当然在线测量技术的广泛应用还有许多问题急待解决，如高精度传感器的研制，测量策略和数据处理策略的优化等，随着这些问题的解决，在线测量技术会有更光明的应用前景。